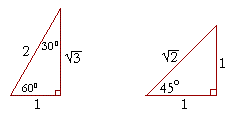Labeled 30 60 90 Triangle Sides

Two of the most common right triangles are 30 60 90 and the 45 45 90 degree triangles all 30 60 90 triangles have sides with the same basic ratio if you look at the 30 60 90 degree triangle in radians it translates to the following. For hypotenuse c known the legs formulas look as follows. Knowledge of the ratio of the le.

în această situaţie veţi circula cu lagărul de concentrare buchenwald în ce situație se interzice circulația autovehiculelor pe drumurile publice lapte si miere baia mare în care dintre situații oprirea este interzisă laptisor de matca pret catena lapte de magarita kaufland pret lake shore drive apartments chicago 1951 mies van der rohe plan

The Easy Guide To The 30 60 90 Triangle

The Complete Guide To The 30 60 90 Triangle

Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

30 60 90 Right Triangles Free Math Help

Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

30 60 90 Triangles

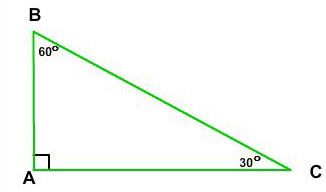
A 30 60 90 triangle is shown below.

Labeled 30 60 90 triangle sides. Part 1 part 2 the length of the hypotenuse is 6 units. One is the 30 60 90 triangle. Our final answer is 8 3. The 30 60 90 triangle is one example of a special right triangle.

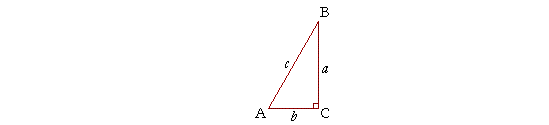
30 60 90 triangle sides. They are special because with simple geometry we can know the ratios of their sides. Learn about special right triangles. We can see why these relations should hold by plugging in the above values into the pythagorean theorem a 2 b 2 c 2.

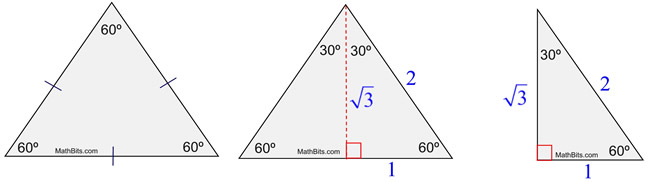
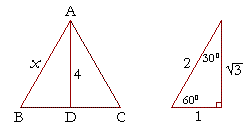
Imagine cutting an equilateral triangle vertically right down the middle. The hypotenuse is the longest side in a right triangle which is different from the long leg. If we know the shorter leg length a we can find out that. The side lengths and angle measurements of a 30 60 90 right triangle.

We will prove that below. In a 30 60 90 triangle the sides are in the ratio 1. If the longer leg length b is the one parameter given then. Now when we are done with the right triangle and other special right triangles it is time to go through the last special triangle which is 30 60 90 triangle.

Add your answer and earn points. It also carries equal importance to 45 45 90 triangle due to the relationship of its side. A special right triangle is a right triangle having angles of 30 60 90 or 45 45 90. It has two acute angles and one right angle.

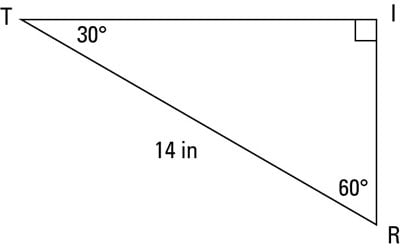
1 see answer sackofawsomeness is waiting for your help. It is right triangle whose angles are 30 60 and 90. The following diagram shows a 30 60 90 triangle and the ratio of the sides. Scroll down the page for more examples and solutions on how to use.

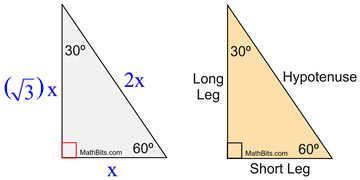
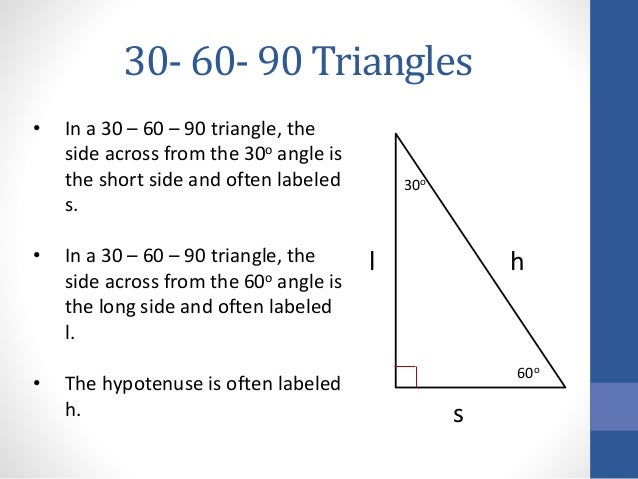
Each half has now become a 30 60 90 triangle. A 30 60 90 triangle is a special right triangle that contains internal angles of 30 60 and 90 degrees. Find the length of the side labeled y. The long leg is the leg opposite the 60 degree angle.

There are two special triangles in trigonometry. Once we identify a triangle to be a 30 60 90 triangle the values of all angles and sides can be quickly identified. A 2 3a 2 4a 2. And because this is a 30 60 90 triangle and we were told that the shortest side is 8 the hypotenuse must be 16 and the missing side must be 8 3 or 8 3.

A 2 a 3 2 2a 2. The lengths of the sides of a 30 60 90 triangle are in the ratio of 1 3 2. Remembering the rules for 30 60 90 triangles will help you to shortcut your way through a variety of math problems. The other is the isosceles right triangle.

30 60 90 triangle explanation examples.